Логические схемы (схемы из функциональных элементов)
Многие элементы в современной электронике являются устройствами, преобразующими некоторые входные сигналы (данные) в выходные. Логические схемы, в отечественной литературе чаще называемые схемами из функциональных элементов, представляют собой математическую модель таких устройств, в которых временем выполнения преобразования входов в выходы можно пренебречь.
Чтобы не усложнять определение, зафиксируем конкретный базис B0={


Определение 2.1. Логической схемой (схемой из функциональных элементов) в базисе B0 называется размеченный ориентированный граф без циклов S=(V,E), в котором
вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);в каждую из остальных вершин входит одно или два ребра; вершины, в которые входит одно ребро помечены функцией ¬, а вершины, в которые входят по два ребра, - одной из функций


Как и для деревьев, для ориентированных графов без циклов можно естественным образом ввести понятие глубины.
Определение 2.2. Глубина вершины v

Глубиной D(S) схемы S назовем максимальную из глубин ее вершин.
Пусть входы схемы S помечены переменными x1, … , xn. С каждой вершиной v

Определение 2.3.
Базис: v имеет глубину 0. Тогда это входная вершина, которая помечена некоторой переменной xi. Положим fv(x1,… , xn) = xi.
Шаг индукции. Пусть всем вершинам w глубины

если v помечена ¬ и в нее входит ребро (w,v) , то положим

если v помечена


если v помечена


Нетрудно понять, что шаг индукции в этом определении корректен, так как, если в схеме S имеется ребро (w,v) и глубина вершины v равна k+1, то глубина вершины w не превосходит k и для нее fw уже определена по индукционному предположению.
Определение 2.4. Схема S реализует набор булевых функций g1, g2, … , gm, если для каждого i


Замечание. Определение логических схем естественным образом можно распространить и на другие базисы. При этом, однако, для вершин, помеченных несимметричными функциями ( например, импликацией), нужно явно нумеровать входящие в них ребра, указывая, каким аргументам они соответствуют.
Определение 2.5. Сложность L(S) схемы S - это число функциональных элементов в S. Сложность L(f) булевой функции f(x1, …, xn) - это наименьшая из сложностей схем, реализующих эту функцию.
Отношения между булевыми функциями и схемами естественно приводят к двум следующим основным проблемам.
Проблема анализа: по заданной схеме из функциональных элементов и выделенному подмножеству ее выходных вершин определить булевы функции, реализуемые в этих вершинах.
Проблема синтеза: по некоторому описанию булевой функции построить схему из функциональных элементов, реализующую эту функцию. При решении проблемы синтеза для исходной функции часто стараются построить схему минимальной или почти минимальной сложности.
Пример 2.1. Рассмотрим схему S1
с тремя входными переменными x, y и z, изображенную на рис. 2.1 и решим для нее проблему анализа.
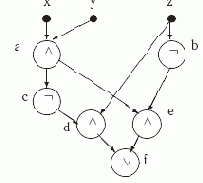
Рис. 2.1. Схема S1
В соответствии с данным выше определением вершины схемы S1 реализуют следующие функции:
fa(x,y,z) = x














Глубина этой схемы D(S1)= 4, а ее сложность L(S1)=6. В то же время формула для результирующей функции ff содержит 7 функциональных знаков. За счет чего достигнута экономия? За счет того, что функция (x

В этом и состоит основное преимущество вычислений булевых функций схемами: каждую подформулу (подфункцию) достаточно вычислить один раз, а затем полученное значение можно использовать сколько угодно раз в качестве аргумента для других подфункций.
Схемы и линейные программы
Указанное выше свойство характерно и для программ, в которых один раз вычисленное значение выражения можно использовать неоднократно. Рассмотрим один из простейших классов программ - линейные или неветвящиеся программы. Такие программы представляют последовательности присваиваний вида:

где X, X1, … , Xk - переменные, F - имя k-местной базисной функции.
В случае нашего базиса B0={




Линейная программа P с выделенными входными переменными X1, … , Xn
порождает для каждого набора ?1, …, ?n значений входных переменных естественный процесс вычисления: вначале переменным X1, … , Xn присваиваются значения ?1, …, ?n, соответственно, а каждой из остальных переменных присваивается значение 0. Затем последовательно выполняются присваивания программы P, в результате чего каждая из переменных Z программы получит заключительное значение PZ(?1, …, ?n).
Определение 2.6.
Скажем, что программа P со входными переменными X1, … , Xn
вычисляет в выходной переменной Z функцию F(X1, …, Xn), если для любого набора значений входов ?1, …, ?n после завершения работы PZ(?1, …, ?n)=F(?1, …, ?n) .
Между схемами и линейными программами имеется тесная связь.
Теорема 2.1.
По каждой логической схеме S со входами x1, … , xn и функциональными элементами v1, …, vm можно эффективно построить линейную программу PS со входными переменными x1, … , xn и рабочими переменными v1, …, vm, которая в любой переменной vi, i=1,…,m, вычисляет функцию

Доказательство. (1) Пусть S - схема со входами x1, … , xn и функциональными элементами v1, …, vm. Построим по ней линейную программу PS со входными переменными x1, … , xn следующим образом. Упорядочим все входные и функциональные вершины S по глубине (вершины одной глубины в любом порядке): u1, …, un+m.
Программа PS будет последовательностью m присваиваний.
Пусть вершина un+i помечена ¬ и в нее входитребро из uj. Тогда в качестве i-ой команды поместим в PS присваивание un+i= ¬ uj.Пусть вершина un+i помечена \circ



Упорядочение вершин по глубине гарантирует, что j <n+ i и k <n+ i. Поэтому при вычислении u_{n+i} значения аргументов уже получены и индукцией по глубине легко показать, что для каждого i=1,…,m программа PS вычисляет в переменной vi функцию

Доказательство пункта (2) проведите самостоятельно (см. задачу 2.1).
Пример 2.1.
Применим конструкцию теоремы к схеме S1, представленной на рис.2.1. Ее вершины можно упорядочить по глубине так: x, y, z, a, b, c, d, e, f. Порождая команды по описанным выше правилам, получим следующую линейную программу P_{S1}:

Замечание. Число команд в линейной программе PS, т.е. время ее выполнения, совпадает со сложностью L(S) схемы S. Глубина схемы D(S) также имеет смысл с точки зрения времени вычисления. Именно, D(S) - это время выполнения PS на многопроцессорной системе. Действительно, все команды, соответствующие вершинам одинаковой глубины, можно выполнять параллельно на разных процессорах, так как результаты любой из них не используются в качестве аргументов другой.
Рассмотрим схему S+ на рис.
Рассмотрим схему S+ на рис. 2.2.
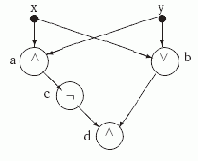
Рис. 2.2. Схема S+ для функции x+y
В соответствии с определением вершины этой схемы реализуют следующие функции:
fa(x,y) = x







Таким образом, схема S+ реализует (в вершине d) функцию + сложения по модулю 2.
Из приведенного выше примера следует, что L(S+)=4 и L(+)

Используя схему S+, нетрудно построить схему Sodd для реализации линейной функции-суммы n аргументов по модулю 2 odd(X1,X2,…, Xn)= X1 +X2 +… + Xn (см. рис. 2.3).
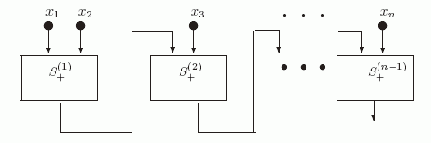
Рис. 2.3. Схема Sodd
На этой схеме прямоугольники S+(1), S+(2), … ,S+(n) содержат копии схемы S+. При этом входами S+(1) являются переменные x1 и x2, а входами S+(i+1) являются выход схемы S+(i) и переменная xi+1. По индукции легко показать, что вершина d в S+(i) реализует функцию (x1 + x2 + … + xi+1). Таким образом, нами установлена
Теорема 2.2.
Существует схема Sodd, реализующая функцию odd(X1,X2,…, Xn)= X1 +X2 +… + Xn
со сложностью L(Sodd)= 4 (n-1).
Сумматор
Сумматором порядка n называют схему, вычисляющую результат сложения двух n-разрядных двоичных чисел



( здесь ai, bi, ci


Сумматор должен вычислять набор из (n+1)-ой результирующей функции:

задающих соответствующие разряды суммы c.
Обозначим через pi бит переноса из (i-1)-го разряда в i-ый. Тогда нетрудно видеть, что при i =0
c0 = a0 + b0 и p1 = a0

а при 1


ci= pi + ai + bi и pi+1 = (ai





Старший разряд c совпадает с последним переносом: cn=pn.
Рассмотрим теперь построенную выше схему S+ как схему, вычисляющую набор из двух функций: x



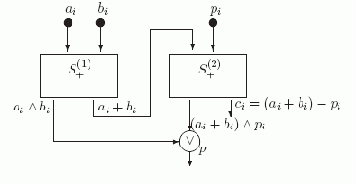
Рис. 2.4. Схема SUM1
Действительно, из построения следует, что в вершине p этой схемы вычисляется функция fp = (ai








Теперь из S+ и одноразрядных сумматоров SUM1 соберем схему SUMn для n-разрядного сумматора.
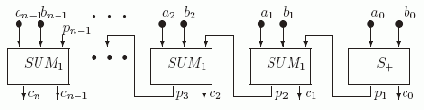
Рис. 2.5. Схема cумматора SUMn
Таким образом мы установили следующее утверждение.
Теорема 2.3.
Для каждого n

Замечание Логические схемы интенсивно исследовались 50-х-70-х годах прошлого столетия. В частности, К. Шеннон и О.Б. Лупанов установили оценки сложности схем для булевых функций от n аргументов. Оказалось, что любую такую функцию можно реализовать со сложностью не большей (по порядку) 2n/n и что "почти все" они имеют не меньшую сложность. При этом до сих пор не известна ни одна последовательность "конкретных" функций fn, сложность которых по порядку превосходила бы линейную функцию.
что минимальная схема для сложения
Задача 2.1. Докажите пункт (2) теоремы 2.1.
Задача 2.2. Докажите, что минимальная схема для сложения имеет сложность L(+) = 4.
Задача 2.3. Используя схему SUMn, постройте схему, реализующую операцию вычитания двух n-разрядных двоичных чисел: d =a - b (при условии, что a

Задача 2.4. Определите глубину схем S+, Sodd, SUM1 и SUMn.
Задача 2.5. Два игрока независимо выбирают одно из четырех чисел от 0 до 3. Первый игрок выигрывает, если выбранные числа совпадают. Постройте схему, определяющую выигрыш 1-го игрока. Ее входы x1,x2 представляют число, выбранное 1-ым игроком, а y1,y2 - число, выбранное 2-ым игроком. Реализуемая функция F(x1,x2,y1,y2) равна 1 тогда и только тогда, когда x1=y1 и x2 =y2.
Задача 2.6. Постройте схему, определяющую результат голосования в комитете, состоящем из трех членов и председателя. В случае равенства голосов, голос председателя является решающим.
Задача 2.7. Пусть наборы аргументов булевой функции от трех аргументов упорядочены лексикографически, а ее значения задаются последовательностью 8 нулей и единиц. Постройте схемы, реализующие следующие функции.
f1=(1111 1011),f2=(1001 1001), f3 =(0011 1001).
